Cohen量子力学Chap.4：自旋1/2和二能级系统

本章将会对第三章所提出的假定进行初步的简单应用，即以两个二维态空间的问题为例来深刻理解这些假定所直接导致的量子效应。

自旋为 ${\frac{1}{2} }$ 的粒子：角动量量子化

斯特恩-盖拉赫实验

斯特恩-盖拉赫实验设计了一个特殊的磁场环节，它沿 $y$ 轴均匀分布，关于 $yOz$ 平面对称分布，且 $B_y=0$ ， $\boldsymbol B(x,y,z)= \boldsymbol B(x,z)$ 。设计的核心是满足两个条件： $B_z>0$ 、 $\partial B_z/\partial z<0$ ，即直观来讲，下方的磁场比上方的磁场更强。

现令一束沿着 $Oy$ 方向、且在面 $yOz$ 内的银原子穿过该磁场区域，最后冷凝于置于磁场前方的板 $P$ 上。显然可以预期，银原子束的行进方向会发生偏转。下面来从经典角度尝试计算这一偏转。

首先，银原子整体是电中性的，不受洛伦兹力。但是它们（由于是顺磁性的）具有永久磁矩 ${\mathscr M}$ ，由此在磁场中具有势能

$$W=-{\mathscr M}\cdot \boldsymbol B$$

对于原子而言，它的磁矩 ${\mathscr M}$ 与角动量 ${\mathscr S}$ 的来源有：电子绕核的运动（轨道磁矩和轨道角动量），以及内禀的“自旋”（自旋磁矩和自旋角动量）。在原子的特定能级中两者存在正比关系：

$${\mathscr M}=\gamma{\mathscr S}$$

比例系数称作该能级的“旋磁比”。

在经过磁场之前，银原子束中各个银原子的磁矩取向应当是各向同性、随机分布的。具体对某一确定的磁矩 ${\mathscr M}$ ，根据势能表达式可知其所受合力（仅在磁场非均匀时存在）为

$$\boldsymbol F=\nabla({\mathscr M}\cdot \boldsymbol B)$$

以及合力矩

$$\boldsymbol \varGamma={\mathscr M}\times \boldsymbol B$$

根据角动量定理可知

$$\frac{ {\rm d}{\mathscr S} }{ {\rm d}t}=\boldsymbol \varGamma=\gamma{\mathscr S}\times \boldsymbol B$$

这一方程，形象来讲，描述了这样一种运动，即磁场使得磁矩矢量 ${\mathscr M}$ 或角动量矢量 ${\mathscr S}$ 绕着磁感应矢量 $\boldsymbol B$ 旋转，但是并不改变大小，也不改变矢量间的夹角。旋转的角速度就是 $\gamma \boldsymbol B$ 。

想要从这个方程中计算银原子受到的合外力 $\boldsymbol F$ ，可取一近似：由于上述旋转频率一般而言较高，因此磁矩垂直于磁感线的分量 $\mathscr M_x$ 、 $\mathscr M_y$ 的作用迅速被时间平均所抹掉（它们的时间期望为零）；而 $\mathscr M_z$ 又是恒定的。整体而言在一段时间的期望下合外力相当于

$$\boldsymbol F=\nabla(\mathscr M_zB_z)=\mathscr M_z\nabla B_z$$

而 $\nabla B_z=\left(\frac{\partial B_z}{\partial x},\frac{\partial B_z}{\partial y},\frac{\partial B_z}{\partial z}\right)$ 这一部分，由于银原子束在面 $yOz$ 内，该面为对称面，因而面上各店的 $\partial B_z/\partial x=0$ ；同时 $\partial B_z/\partial y=0$ ，因此

$$\boldsymbol F=\mathscr M_z\frac{\partial B_z}{\partial z}{\hat z}$$

可见这就产生了使得银原子束偏转的力。考虑到银原子磁矩取向的随机性，其分量 $\mathscr M_z=\mathscr M\cos\theta$ ，其中 $\theta$ 是经典模型中 ${\mathscr M}$ 和 $\boldsymbol B$ 的夹角。由于磁矩取向是随机的，因而这一夹角也是随机的，故 $\mathscr M_z$ 的取值均匀分布于一个区间即 $-|{\mathscr M}|\sim+|{\mathscr M}|$ 。但是由于这一区间尺寸较小，总体来说各个银原子的偏转方向应当是近似一致的，对应于板上形成单个银原子冷凝的小斑点，其位置应当处于 $+z$ 方向。换句话说，在经典理论中，偏转距离（用板中心 $z=0$ 处的点 $N$ 与冷凝斑点中心 $H$ 标记） $NH$ ，唯一地决定于 $\mathscr M_z$ 或 $\mathscr S_z$ 。

但是斯特恩-盖拉赫实验得到的结果却和前述的经典计算相矛盾：事实上在板上发现了两处斑点，且其位置 $H_1$ 、 $H_2$ 关于中心点处上下对称。

这表明量子力学的实际理论与经典理论存在巨大差异。回顾一下前面的理论分析并考虑这样一个问题：前面涉及到的银原子的各种物理量，可以分为两类，一是可由位置 $\boldsymbol r$ 和动量 $\boldsymbol p$ 完全决定的，称为“外部自由度”；另一类则是角动量或磁矩这一类，称为“内部自由度”。

首先，外部自由度不必用精确的量子力学来处理。这是因为根据之前的分析，我们可以用波包放在经典框架中计算微观粒子的运动行为，而在实验的尺度下这些波包的宽度都可以忽略。因此本实验中，经典理论与实验结果的差异，不应当出在外部自由度上。同时这也肯定了，“板上的冷凝位置对应于银原子的 $\mathscr M_z$ 或 $\mathscr S_z$ ”这一结论是没有问题的。

但是另一方面，却没有足够的证据表明我们可以对内部自由度做同样的事情，即采用经典模型计算。因此实验结果迫使我们得出结论：如果测量基态银原子的内禀角动量分量 $\mathscr S_z$ ，那么将会得到两个相反的值其中的一个，分别对应于板上的两个冷凝斑点 $H_1$ 、 $H_2$ 。这就是说，对于角动量分量 $\mathscr S_z$ 或磁矩分量 $\mathscr M_z$ 的测量，不能再采用 $\mathscr M_z=\mathscr M\cos\theta$ 的经典连续图像，而要认为它是量子化的物理量，其离散谱只包含两个相反的本征值（或者说，目前至少认为是两段处于相反位置上很窄的区间）。根据这一结果，称基态银原子为“自旋 $\frac12$ ”的。

理论描述

下面将会针对上面的现象，对所谓“自旋 $\frac12$ ”的粒子初步地建立物理模型，即了解量子力学是如何描述这类粒子的。

可观测量 $S_z$ 和自旋态空间

首先对于自旋角动量 $z$ 分量 $\mathscr S_z$ ，应当联系于一个观察算符 $S_z$ ，它具有两个相反的非简并的本征值。后面的研究将会看到，它们分别是 $+\frac\hbar2$ 和 $-\frac\hbar2$ ，对应的本征矢分别记作 $|+\rangle$ 和 $|-\rangle$ ，即

$$\left\{\begin{aligned} S_z|+\rangle=+\frac\hbar2|+\rangle\\ S_z|-\rangle=-\frac\hbar2|-\rangle \end{aligned}\right.$$

且

$$\left\{\begin{aligned} &\langle+|+\rangle=\langle-|-\rangle=1\\ &\langle+|-\rangle=0 \end{aligned}\right.$$

因此 $S_z$ 本身就构成一个CSCO，其态空间是二维的， $|+\rangle 和 |-\rangle$ 构成一个基，封闭性关系 $|+\rangle\langle+|+|-\rangle\langle-|=I$ 。在这个基下 $S_z$ 具有对角形式的矩阵

$$[S_z]=\frac\hbar2\begin{bmatrix}1&0\\0&-1\end{bmatrix}$$

自旋的其他可观测量

自旋角动量的另外两个分量 $\mathscr S_x$ 、 $\mathscr S_y$ 分别对应于观察算符 $S_x$ 、 $S_y$ 。由于 $S_z$ 本身就构成一个CSCO，因此在它的本征矢构成的基 $\{|+\rangle,|-\rangle\}$ 下，算符 $S_x$ 、 $S_y$ 也可以表示成 $2\times 2$ 的厄米算符形式。实际上根据角动量经典力学中角动量分量所满足的代数关系（即所谓“角动量代数” $\mathfrak{so}_3$ ）

$$[\mathscr S_i,\mathscr S_j]={\rm i}\varepsilon_{ij}^k\mathscr S_k$$

可以合理猜测（并且后面证明）：

$$[S_x]=\frac\hbar2\begin{bmatrix}0&1\\1&0\end{bmatrix}$$ $$[S_y]=\frac\hbar2\begin{bmatrix}0&-{\rm i}\\{\rm i}&0\end{bmatrix}$$

实际上它们就是泡利矩阵在泡利表象（ $\sigma_z$ 表象）下的表示：

$$\sigma_x=\begin{bmatrix}0&1\\1&0\end{bmatrix}\quad\sigma_y=\begin{bmatrix}0&-{\rm i}\\{\rm i}&0\end{bmatrix}\quad\sigma_z=\begin{bmatrix}1&0\\0&-1\end{bmatrix}$$

更一般地，对于在极角为 $(\theta,\varphi)$ 的单位矢量 $\boldsymbol u$ 方向上，总角动量 ${\mathscr S}$ 的分量：

$$\mathscr S_u={\mathscr S}\cdot\boldsymbol u=\mathscr S_x\sin\theta\cos\varphi+\mathscr S_y\sin\theta\sin\varphi+\mathscr S_z\cos\theta$$

因此相应的观察算符 $S_{\boldsymbol u}$ 在基 $\{|+\rangle,|-\rangle\}$ 下的矩阵表示为

$$[S_{\boldsymbol u}]=\frac\hbar2\begin{bmatrix}\cos\theta&\sin\theta{\rm e}^{-{\rm i}\varphi}\\\sin\theta{\rm e}^{ {\rm i}\varphi}&-\cos\theta\end{bmatrix}$$

下面考虑算符 $S_x$ 、 $S_y$ 、 $S_u$ 的本征问题。很显然它们的本征值都是 $\pm\frac\hbar2$ ；这在物理上其实就相当于是将实验的整个系统旋转一下到平行于另一个轴，自然实验结果不应该变化，即本征值都是相同的。因此相应地，也可以分别用 $+$ 、 $-$ 来标记相应的两个本征矢。将算符 $S_x$ 、 $S_y$ 、 $S_u$ 的本征矢分别记为 $|\pm\rangle_x$ 、 $|\pm\rangle_y$ 、 $|\pm\rangle_u$ ，则它们分别可以由 $S_z$ 的本征矢 $|\pm\rangle$ 表示为

$$|\pm\rangle_x=\frac1{\sqrt2}\big[|+\rangle\pm|-\rangle\big]$$ $$|\pm\rangle_y=\frac1{\sqrt2}\big[|+\rangle\pm{\rm i}|-\rangle\big]$$ $$\left\{\begin{aligned} &|+\rangle_{\boldsymbol u}=\cos\frac\theta2{\rm e}^{-{\rm i}\frac\varphi2}|+\rangle+\sin\frac\theta2{\rm e}^{ {\rm i}\frac\varphi2}|-\rangle\\ &|-\rangle_{\boldsymbol u}=-\sin\frac\theta2{\rm e}^{-{\rm i}\frac\varphi2}|+\rangle+\cos\frac\theta2{\rm e}^{ {\rm i}\frac\varphi2}|-\rangle \end{aligned}\right.$$

就自旋为 ${\frac{1}{2} }$ 的情况说明量子力学的假定

各自旋态的制备

自旋态 $|+\rangle$ 和 $|-\rangle$ 的制备

算符 $S_z$ 的本征态的制备非常简单。只要利用斯特恩-盖拉赫实验的结果，在右侧选择性地分别让向上偏转或向下偏转的银原子束通过，例如在原有冷凝位置开孔，那么它们分别就全部处于是 $|+\rangle$ 态或 $|-\rangle$ 态。

这是因为“通过右侧板”这一事件本质上相当于是对通过磁场区域的银原子的角动量 $z$ 分量 $\mathscr S_z$ 进行了观测。通过上孔的银原子的观测结果自然是 $+\frac\hbar2$ ，由于 $S_z$ 构成CSCO，于是银原子确定处于态 $|+\rangle$ ；反之同理。因此实际上这套设备对于银原子所起的作用相当于是某种“原子起偏器”，类似于光学起偏器是将任意偏振成分的光通过后变为某一偏振光。

自旋态 $|\pm\rangle_x$ 、 $|\pm\rangle_y$ 、 $|\pm\rangle_u$ 的制备

只要将系统的设备进行旋转，使其银原子束发出的方向分别平行于 $Ox$ 轴、 $Oy$ 轴、单位矢量 $\boldsymbol u$ ，由于相应的算符 $S_x$ 、 $S_y$ 、 $S_u$ 也都分别构成CSCO，因此可以完全类似 $S_z$ 的处理进行态的制备。

一般自旋态的制备

自旋态空间中一般的右矢具有形式：

$$|\psi\rangle=\alpha|+\rangle+\beta|-\rangle\quad(|\alpha|^2+|\beta|^2=1)$$

模长方面，事实上一定存在唯一的 $\theta\in[0,\pi]$ 满足：

$$\left\{\begin{aligned}\cos\frac\theta2&=|\alpha|\\ \sin\frac\theta2&=|\beta|\end{aligned}\right.$$

而相位方面，根据前面的结论，存在物理效应的仅仅是 $\alpha$ 、 $\beta$ 的相位差，因此可令

$$\left\{\begin{aligned}\varphi=\arg\beta-\arg\alpha\\ \chi=\arg\beta+\arg\alpha\end{aligned}\right.$$

于是

$$\left\{\begin{aligned}\arg\alpha=\frac12\chi-\frac12\varphi\\ \arg\beta=\frac12\chi+\frac12\varphi\end{aligned}\right.$$

利用这些记号，有

$$|\psi\rangle={\rm e}^{ {\rm i}\frac\chi2}\left[\cos\frac\theta2{\rm e}^{-{\rm i}\frac\varphi2}|+\rangle+\sin\frac\theta2{\rm e}^{ {\rm i}\frac\varphi2}|+\rangle\right]$$

可见对于任意的自旋态 $|\psi\rangle$ ，总存在一个单位矢量 $\boldsymbol u’$ 所决定的方向，使得它与 $|+\rangle_{\boldsymbol u’}$ 只相差一个没有物理意义的相位因子。

自旋的测量

前面的讨论表明，利用斯特恩-盖拉赫实验设备可以测量银原子的角动量在指定方向上的分量；另一方面也可以用来制备指定的自旋态。因此两套实验设备级联放置，实际上就可以构成一种类似于光学中的“检偏设备”，用以验证前面提出的量子力学模型。

实验假定两套设备安排很近且无其他干扰，使得银原子在两套设备之间运动过程中自旋态不会发生改变。

同向级联设备实验

现使两套设备的轴线均平行于$Oz$轴。第一套设备的作用是制备处于态 $|+\rangle$ 的原子，第二套设备测量其 $\mathscr S_z$ 。根据量子力学的假定，进入第二套设备的银原子全部处于本征态 $|+\rangle$ ，因而测量结果一定是本征值 $+\frac\hbar2$ ，因而所有银原子都应该冷凝到同一个斑点处。实验结果与理论预测一致。

异向级联设备实验一

现在前一实验基础上调整第一套设备，使其轴线平行于极角 $(\theta,\varphi=0)$ 的单位矢量 $u$ （即位于 $xOz$ 面内），而保持第二套设备轴线方向不变。于是从“起偏器”发出的原子自旋态都处于

$$|\psi\rangle=\cos\frac\theta2|+\rangle+\sin\frac\theta2|-\rangle$$

那么在经过第二套设备后，理论将会预期，原子有 $p_+=\cos^2\frac\theta2$ 的概率测量值为 $+\frac\hbar2$ ，落到上冷凝点；有 $p_-=\sin^2\frac\theta2$ 的概率测量值为 $-\frac\hbar2$ ，落到下冷凝点；因而当原子数目较多的时候，上下冷凝点处的原子数目应当分别正比于 $\cos^2\frac\theta2$ 和 $\sin^2\frac\theta2$ 。实验结果证明了这一预测。

异向级联设备实验二

第一台设备按上述调整，同时将第二套设备的轴线调整为平行于 $Ox$ 轴，即对于态

$$|\psi\rangle=\cos\frac\theta2|+\rangle+\sin\frac\theta2|-\rangle$$

测量其角动量 $x$ 分量 $\mathscr S_x$ 。可以计算得

$$\left\{\begin{aligned}_x\langle+|\psi\rangle=\frac1{\sqrt2}\left(\cos\frac\theta2+\sin\frac\theta2\right)=\cos\left(\frac\pi4-\frac\theta2\right)\\_x\langle-|\psi\rangle=\frac1{\sqrt2}\left(\cos\frac\theta2-\sin\frac\theta2\right)=\sin\left(\frac\pi4-\frac\theta2\right)\end{aligned}\right.$$

可见测量 $\mathscr S_x$ 得到本征值 $\pm\frac\hbar2$ 的概率分别是 $\cos^2\left(\frac\pi4-\frac\theta2\right) 和 \sin^2\left(\frac\pi4-\frac\theta2\right)$ 。关于实验检验，可以通过观察冷凝斑点的强度来验证。 这在物理上是比较好理解的，尤其是出现了角度 $\left(\frac\pi4-\frac\theta2\right)=\frac12\left(\frac\pi2-\theta\right)$ ，因为在上个实验中两套仪器夹角为 $\theta$ ，再将第二套仪器旋转后角度自然就变成 $\left(\frac\pi2-\theta\right)$ 。

平均值

现在回想一下，关于这一实验的量子理论与经典理论之间的关系，实际上应当从均值期望的角度来理解。例如在异向级联设备实验一中，无论 $\theta$ 大小如何（只要不等于 $0$ 或 $\pi$ ），第二套设备测量其 $\mathscr S_z$ 总会出现两个结果： $\pm\frac\hbar2$ 。但是这与经典直觉是相悖的，经典理论给出的结果应当是唯一的，即 $\frac\hbar2\cos\theta$ ，尽管此时实验结果和量子理论都给出了两个结果。尤其是在 $\theta\approx0$ 的情况下经典理论只会给出 $\frac\hbar2\cos\theta\approx\frac\hbar2$ ，但是实验还会测得 $-\frac\hbar2$ 的结果。

实际上，正确的理解应当是从期望角度来解释两者之间的联系，即认为经典结果是对于量子结果的均值描述。若从概率的角度来看的话， $\theta$ 越小，得到 $-\frac\hbar2$ 结果的概率 $\sin^2\frac\theta2$ 也就越小。一般地，在多次（ $N$ 次）全同实验下，测量结果的平均值

$$\langle\mathscr S_z\rangle=\frac1N\left[\frac\hbar2N\cos^2\frac\theta2-\frac\hbar2N\sin^2\frac\theta2\right]=\frac\hbar2\cos\theta$$

这与经典结果是一致的。

实际上这也是算符 $S_z$ 在 $|\psi\rangle$ 下的期望 $\langle S_z\rangle$ ，或者说正是矩阵元 $\langle\psi|S_z|\psi\rangle$ 。同样，

$$\langle \mathscr S_x\rangle=\frac1N\left[\frac\hbar2N\cos^2\left(\frac\pi4-\frac\theta2\right)-\frac\hbar2N\sin^2\left(\frac\pi4-\frac\theta2\right)\right]=\frac\hbar2\sin\theta$$

也等于相应算符 $S_x$ 的矩阵元，例如在基 $\{|+\rangle,|-\rangle\}$ 下计算：

$$\langle\psi|S_x|\psi\rangle=\frac\hbar2 \begin{bmatrix}\cos\dfrac\theta2&\sin\dfrac\theta2\end{bmatrix}\begin{bmatrix}0&1\\1&0\end{bmatrix}\begin{bmatrix}\cos\dfrac\theta2\\\sin\dfrac\theta2\end{bmatrix}=\frac\hbar2\sin\theta$$

可见角动量分量的均值，就是相应算符的期望——矩阵元，这进一步说明了引入相应算符来描述角动量的合理性。

前面得到的两个均值 $\frac\hbar2\sin\theta$ 和 $\frac\hbar2\cos\theta$ ，实际上正是经典理论中模长为 $\frac\hbar2$ 、取向为“起偏器”轴向的经典角动量分别在 $Ox$ 轴和 $Oz$ 轴的分量。更普遍地，若计算三个算符 $S_x$ 、 $S_y$ 、 $S_z$ 在态 $|+\rangle_{\boldsymbol u}$ 中的平均值：

$$\left\{\begin{aligned} _{\boldsymbol u}\langle+|S_x|+\rangle_{\boldsymbol u} &= \frac\hbar2\sin\theta\cos\varphi\\ _{\boldsymbol u}\langle+|S_y|+\rangle_{\boldsymbol u} &= \frac\hbar2\sin\theta\sin\varphi\\ _{\boldsymbol u}\langle+|S_z|+\rangle_{\boldsymbol u} &= \frac\hbar2\cos\theta \end{aligned}\right.$$

可见这些分量角动量的均值，实际上就是经典理论中模长为 $\frac\hbar2$ 、取向为 $(\theta,\varphi)$ 方向的经典角动量（即角动量矢量为 ${\mathscr S}=\left(\frac\hbar2,\theta,\varphi\right)$ ）分别在 $Ox$ 轴、 $Oy$ 轴和 $Oz$ 轴的分量。这进一步说明了“认为经典结果是对于量子结果的均值描述”这一结论。但是：给定一个原子，测量其角动量分量（例如 $\mathscr S_x$ ），绝对不会得到 $\frac\hbar2\sin\theta\cos\varphi$ ，而只可能是 $\pm\frac\hbar2$ 。

现在可以回顾一下关于外部自由度的问题。之前我们的处理方法，是将外部自由度进行经典处理，即将之看作宽度远小于问题所涉及一切线度的波包，这样就可按照经典轨迹来处理。然而这并不意味着经典理论中“轨道的完全确定性”能够沿用，这是因为还存在内部自由度没有被经典处理。事实上我们看到，在实验中轨道至少有两条。这是因为原始的银原子束，它们的初自旋态实际上是两种本征态的叠加，因而初始的波包实际上可以看作两个具有确定自旋本征态波包的叠加，在经过磁场时“分裂”了，自然产生了两条不同的轨迹。

自旋 ${\frac{1}{2} }$ 粒子的态在均匀磁场中的演变

相互作用的哈密顿算符和薛定谔方程

考虑一个置于均匀磁场 $\boldsymbol B_0=B_0\hat z$ 中的银原子，则其经典势能为

$$W=-{\mathscr M}\cdot\boldsymbol B_0=-\mathscr M_zB_0=-\gamma B_0\mathscr S_z$$

令 $\omega_0=-\gamma B_0$ ，它具有角频率的量纲。量子力学仅对研究对象量子化而不对环境场量子化，因而将内部自由度量子化后，经典能量变为哈密顿算符：

$$H=\omega_0S_z$$

它描述原子的自旋在均匀静态磁场中的演变。
注：若 $\boldsymbol B_0=B_0\hat u$ ，则 $H=\omega_0S_u$ 。
它与时间无关，于是系统演化完全取决于它的本征方程。显然它的本征矢就是 $S_z$ 的本征矢：

$$\left\{\begin{aligned}H|+\rangle=+\frac{\hbar\omega_0}2|+\rangle\\ H|-\rangle=+\frac{\hbar\omega_0}2|-\rangle\end{aligned}\right.$$

于是这将会是一个二能级系统： $E_+=+\frac{\hbar\omega_0}2$ ， $E_-=-\frac{\hbar\omega_0}2$ 。能级差 $\hbar\omega_0$ 与磁场强度成正比，且唯一确定了一个波尔频率：

$$\nu_{+-}=\frac{E_+-E_-}\hbar=\frac{\omega_0}{2\pi}$$

拉莫尔进动

设在 $t=0$ 时刻粒子的自旋态是

$$|\psi(0)\rangle=\cos\frac\theta2{\rm e}^{-{\rm i}\frac\varphi2}|+\rangle+\sin\frac\theta2{\rm e}^{ {\rm i}\frac\varphi2}|-\rangle$$

（任一自旋态都可写成这种形式），那么利用定态展开计算任意 $t>0$ 时刻的自旋态：

$$\begin{aligned}|\psi(t)\rangle&=\cos\frac\theta2{\rm e}^{-{\rm i}\frac\varphi2}{\rm e}^{-{\rm i}\frac{E_+t}\hbar}|+\rangle+\sin\frac\theta2{\rm e}^{ {\rm i}\frac\varphi2}{\rm e}^{-{\rm i}\frac{E_-t}\hbar}|-\rangle\\ &=\cos\frac\theta2{\rm e}^{-{\rm i}\frac{\varphi+\omega_0t}2}|+\rangle+\sin\frac\theta2{\rm e}^{ {\rm i}\frac{\varphi+\omega_0t}2}|-\rangle\end{aligned}$$

可见磁场 $\boldsymbol B_0$ 的存在使得右矢 $|+\rangle$ 和 $|-\rangle$ 的展开系数之间分别出现与时间成正比的相移。

再考虑上式，其实可以表示为某一方向角动量分量的本征矢 $|+(t)\rangle_{u(t)}$ ，换句话说上面的随时间演化的自旋态，在由

$$\left\{\begin{aligned}&\theta(t)=\theta\\&\varphi(t)=\varphi+\omega_0t\end{aligned}\right.$$

方向所决定的单位矢量 $u(t)$ 上的分量一定为 $+\frac\hbar2$ 。极角表明， $\boldsymbol u(t)$ 与 $\boldsymbol B_0$ 的方向之间的夹角 $\theta$ 保持不变，但却又以正比于 $B_0$ 大小的角速度 $\omega_0$ 绕其旋转，这个现象叫做拉莫尔进动。

从哈密顿算符的表达式也可看出，可观测量 $S_z$ 是一个运动常量（与之对易），对其观测一次得到的结果为 $+\frac\hbar2$ 或 $-\frac\hbar2$ 的概率与时间无关，因为 $\left|{\rm e}^{\pm{\rm i}\frac{\varphi+\omega_0t}2}\right|=1$ ；从而它的均值也不依赖于时间

$$\langle\psi(t)|S_z|\psi(t)\rangle=\frac\hbar2\cos\theta$$

但是 $S_x$ 、 $S_y$ 都不与 $H$ 对易，有

$$\langle\psi(t)|S_x|\psi(t)\rangle=\frac\hbar2\sin\theta\cos(\varphi+\omega_0t)$$ $$\langle\psi(t)|S_y|\psi(t)\rangle=\frac\hbar2\sin\theta\sin(\varphi+\omega_0t)$$

这正反映了前面得到的系统唯一的玻尔频率 $\omega_0/2\pi$ 。

二能级体系的一般研究

上述均匀磁场中的自旋 $\frac12$ 粒子是一个典型的二能级系统。很多问题可以被近似为二能级系统，进而计算外界微扰对其影响。或者在一些多能级系统中，一级近似下可以不考虑其他能级对某两个能级的影响。这样通常系统的态空间就是二维的（或者是某个高维空间的二维子空间），从而大大简化运算。

问题的梗概

在二维态空间中，选择哈密顿算符 $H_0$ 的分别属于本征值（即两个能级） $E_1$ 、 $E_2$ 的、且正交归一的两个本征态 $|\varphi_1\rangle$ 、 $|\varphi_2\rangle$ 作为基，则 $H_0$ 可对角化为

$$H_0=\begin{bmatrix}E_1&0\\0&E_2\end{bmatrix}$$

现在考虑对系统做一外界微扰，或是考虑内部相互作用，使得哈密顿算符变为

$$H=H_0+W$$

且具有本征方程

$$\begin{aligned} H|\psi_+\rangle=E_+|\psi_+\rangle\\ H|\psi_-\rangle=E_-|\psi_-\rangle \end{aligned}$$

通常 $H_0$ 叫做未经微扰的哈密顿算符， $W$ 叫做微扰或耦合，这里假定其不依赖于时间。在未微扰的态组成的基 $\{|\varphi_1\rangle,|\varphi_2\rangle\}$ 下它表示为一个厄米矩阵

$$W=\begin{bmatrix}W_{11}&W_{12}\\W_{21}&W_{22}\end{bmatrix}\quad W_{11},W_{22}\in\mathbb R;W_{12}={W_{21} }^*$$

下面考虑引入微扰 $W$ 后对原系统两个能级和定态的修正。

静态方面：耦合对体系的定态的影响

在本节，我们所主要讨论的 $W$ 是指系统内部的耦合（相互作用），或是全部相互作用中次要关心的一部分，或是一些来自外界的微扰；一般而言这种耦合或微扰可能相比于其他作用（例如外场，或者主要关心的相互作用）而言较弱，从而在近似的 $H_0$ 当中被忽略掉。但是将会看到，若采取更高阶的近似，那么在 $H$ 中这种被忽略的耦合将会产生不可忽视的修正。

静态方面， $W$ 主要的影响主要是对忽略近似下的系统能级附加一个修正，即 $E_1$ 、 $E_2$ 修正为 $E_+$ 、 $E_-$ 。

$H$ 的本征值及本征态的表示式

在基 $\{|\varphi_1\rangle,|\varphi_2\rangle\}$ 中

$$H=W=\begin{bmatrix}E_1+W_{11}&W_{12}\\W_{21}&E_2+W_{22}\end{bmatrix}$$

将之对角化得到新的本征值为

$$\begin{aligned} E_+=\frac{E_1+W_{11}+E_2+W_{22} }2+\frac{\sqrt{(E_1+W_{11}-E_2-W_{22})^2+4|W_{12}|^2} }2\\ E_-=\frac{E_1+W_{11}+E_2+W_{22} }2-\frac{\sqrt{(E_1+W_{11}-E_2-W_{22})^2+4|W_{12}|^2} }2 \end{aligned}$$

相应的本征矢为

$$\begin{aligned} |\psi_+\rangle=\cos\frac\theta2{\rm e}^{-{\rm i}\frac\varphi2}|\varphi_1\rangle+\sin\frac\theta2{\rm e}^{ {\rm i}\frac\varphi2}|\varphi_2\rangle\\ |\psi_-\rangle=-\sin\frac\theta2{\rm e}^{-{\rm i}\frac\varphi2}|\varphi_1\rangle+\cos\frac\theta2{\rm e}^{ {\rm i}\frac\varphi2}|\varphi_2\rangle \end{aligned}$$

其中

$$\begin{aligned}&\tan\theta=\frac{2|W_{12}|}{E_1+W_{11}-E_2-W_{22} }\\&W_{21}=|W_{21}|{\rm e}^{ {\rm i}\varphi}\end{aligned}$$

显然，当 $W\to 0$ 时， $E_+$ 、 $E_-$ 分别趋向于较高的、较低的原能级。

能级和本征态的修正

进一步讨论之前，应当注意的是，耦合带来的几乎所有值得讨论的特别的效应都源出于 $W$ 的非对角元 $W_{12}={W_{21} }^*$ ；因为假若 $W_{12}=0$ ，那么 $H$ 的本征态就不会改变，只是能级变为 $E_1+W_{11}$ 、 $E_2+W_{22}$ 而已。

因此简单起见，假设 $W$ 是纯非对角的（ $W_{11}=W_{22}=0$ ，或者只需用 $E_1+W_{11}$ 、 $E_2+W_{22}$ 替代 $E_1$ 、 $E_2$ 即可），并引入参量

$$\begin{aligned}&E_m=\frac12(E_1+E_2)\\ &\Delta=\frac12(E_1-E_2)\end{aligned}$$

它们几乎就可以完全描述耦合修正前的二能级系统。则

$$\begin{aligned} &E_+=E_m+\sqrt{\Delta^2+|W_{12}|^2}\\ &E_-=E_m-\sqrt{\Delta^2+|W_{12}|^2}\\ &\tan\theta=\frac{|W_{12}|}\Delta \end{aligned}$$

可见能级的修正非常简单：简言之就是在原能级的基础上，以两能级均值 $E_m$ 为原点，调节了两个能级距离均值的距离： $\Delta\to\sqrt{\Delta^2+|W_{12}|^2}$ 考虑在微扰强度一定的时候，对于不同的二能级系统影响如何。由于 $E_m$ 的作用只是将能级整体“平移”，因而可以只研究能级对 $\Delta$ 的依赖。很显然这是一个双曲线形：

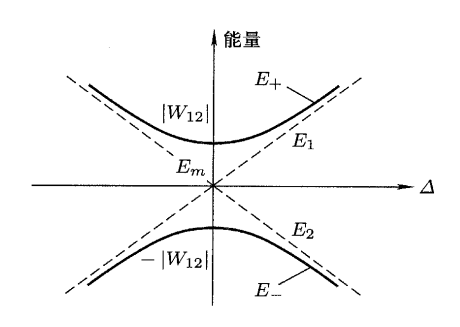
很明显有 $|E_+-E_-|>|E_1-E_2|$ ，即这里出现了一个在很多领域都有的结论：内部的耦合使得系统的固有频率互相远离。

根据 $\Delta$ 和 $|W_{12}|$ 的相对大小，可以将系统的耦合强度分为：强耦合 $\Delta\ll|W_{12}|$ 和弱耦合 $\Delta\gg|W_{12}|$ 。

在弱耦合的区段，能级可以展开为

$$\begin{aligned} &E_+=E_m+\Delta\left(1+\frac12\left|\frac {W_{12} }\Delta\right|^2+\cdots\right)\\ &E_-=E_m-\Delta\left(1+\frac12\left|\frac {W_{12} }\Delta\right|^2+\cdots\right) \end{aligned}$$

反之，在强耦合的区段

$$\begin{aligned} &E_+=E_m+|W_{12}|\\ &E_-=E_m-|W_{12}| \end{aligned}$$

由此可见，耦合对于能量相近的能级修正非常明显，例如在上式，一阶近似就存在耦合的影响；但是对于能量差较大的能级，则影响不甚明显，在二阶或更高的近似中才能看到。
另一方面，讨论本征态的变化。由于 $\tan\theta=\frac{|W_{12}|}\Delta$ ，则强耦合 $\theta\simeq\frac\pi2$ ；弱耦合 $\theta\simeq0$ 。可以看出，对于弱耦合的区段，本征态可以展开为

$$\begin{aligned} &|\psi_+\rangle=\frac1{\sqrt2}\left[{\rm e}^{-{\rm i}\frac\varphi2}|\varphi_1\rangle+{\rm e}^{ {\rm i}\frac\varphi2}|\varphi_2\rangle\right]\\ &|\psi_-\rangle=\frac1{\sqrt2}\left[-{\rm e}^{-{\rm i}\frac\varphi2}|\varphi_1\rangle+{\rm e}^{ {\rm i}\frac\varphi2}|\varphi_2\rangle\right] \end{aligned}$$

反之，在强耦合的区段

$$\begin{aligned} &|\psi_+\rangle={\rm e}^{-{\rm i}\frac\varphi2}\left[|\varphi_1\rangle+{\rm e}^{ {\rm i}\varphi}\frac{|W_{12}|}{2\Delta}|\varphi_2\rangle+\cdots\right]\\ &|\psi_-\rangle={\rm e}^{ {\rm i}\frac\varphi2}\left[|\varphi_2\rangle+{\rm e}^{-{\rm i}\varphi}\frac{|W_{12}|}{2\Delta}|\varphi_1\rangle+\cdots\right] \end{aligned}$$

所以对于本征态来说，弱耦合情况下微扰的影响不大（仅产生一个相位因子）；强耦合情况下微扰则产生了较大影响。

综上可见，无论是对于能级还是本征态，总体来说微扰产生重要修正的情况都是原本能级差较小的系统。这也符合直觉预期。

量子共振现象

当 $E_1=E_2=E_m$ 时， $H_0$ 对应的能量是二重简并的。但是耦合 $W_{12}$ 将会消除这种简并；具体来说产生了两个新的能级，其中之一的能量相对于 $E_m$ 下降了 $|W_{12}|$ （另一个上升 $|W_{12}|$ ），因此任何（纯非对角的）耦合都会降低系统的基态能量，从而使得系统更加稳定。

这一现象经常出现在粒子物理或分子化学当中。存在许多的系统，例如苯分子或 ${\rm H}_2^+$ ，在忽略某些耦合的情况下，它们具有两个能量相等的态（前面两个例子，这两个态分别对应于双键位置的不同，和电子定域在附近的质子的不同）；但同时正是由于内部的耦合，使得系统比预期的更加稳定——这是因为产生了新的基态。这种实际的基态通常可以看作是前述两个态的线性叠加（叠加系数的模相等），从而这就是很多“离域化学键”或“共振化学键”的成因。

动态方面：体系在两个未微扰态之间的振荡

在本节，主要讨论动态方面的问题，即原先的定态 $|\varphi_1\rangle$ 、 $|\varphi_2\rangle$ 将不再是定态（而变成了 $|\psi_+\rangle$ 、 $|\psi_-\rangle$ ）；例如假若 $t=0$ 时刻系统处于 $|\psi_1\rangle$ ，那么在 $t$ 时刻系统有一定的概率 $\mathcal P_{12}(t)$ 处于 $|\psi_2\rangle$ 态。因此可以说， $W$ 引起了两个未微扰态 $|\varphi_1\rangle$ 、 $|\varphi_2\rangle$ 之间的跃迁。正是因此，才称 $W$ 为态 $|\varphi_1\rangle$ 、 $|\varphi_2\rangle$ 之间的耦合。

态矢量的演变； $\mathscr P_{12}(t)$ 的计算：拉比公式

假设在 $t=0$ 时 $|\psi(t)\rangle=|\varphi_1\rangle$ ，则将之在 $H=H_0+W$ 的两个本征态上展开：

$$|\psi(0)\rangle=|\varphi_1\rangle={\rm e}^{ {\rm i}\frac\varphi2}\left[\cos\frac\theta2|\psi_+\rangle-\sin\frac\theta2|\psi_-\rangle\right]$$

于是根据之前的结论

$$|\psi(t)\rangle={\rm e}^{ {\rm i}\frac\varphi2}\left[\cos\frac\theta2{\rm e}^{-{\rm i}\frac{E_+t}\hbar}|\psi_+\rangle-\sin\frac\theta2{\rm e}^{-{\rm i}\frac{E_-t}\hbar}|\psi_-\rangle\right]$$

于是在 $t$ 时刻发现系统处于 $|\psi_2\rangle$ 的概率幅为

$$\begin{aligned}\langle\varphi_2|\psi(t)\rangle&={\rm e}^{ {\rm i}\frac\varphi2}\left[\cos\frac\theta2{\rm e}^{-{\rm i}\frac{E_+t}\hbar}\langle\varphi_2|\psi_+\rangle-\sin\frac\theta2{\rm e}^{-{\rm i}\frac{E_-t}\hbar}\langle\varphi_2|\psi_-\rangle\right]\\&={\rm e}^{ {\rm i}\varphi}\sin\frac\theta2\cos\frac\theta2\left[{\rm e}^{-{\rm i}\frac{E_+t}\hbar}-{\rm e}^{-{\rm i}\frac{E_-t}\hbar}\right]\end{aligned}$$

于是可以计算

$$\begin{aligned}\mathscr P_{12}(t)&=|\langle\varphi_2|\psi(t)\rangle|^2=\frac12\sin^2\theta\left[1-\cos\left(\frac{E_+-E_-}\hbar t\right)\right]\\&=\sin^2\theta\sin^2\left(\frac{E_+-E_-}{2\hbar}t\right)\end{aligned}$$

其中 $\theta$ 满足 $\tan\theta=\frac{2|W_{12}|}\Delta$ 。利用矩阵元还能写成

$$\mathscr P_{12}(t)=\frac{4|W_{12}|^2}{4|W_{12}|^2+(E_1-E_2)^2}\sin^2\left[\sqrt{4|W_{12}|^2+(E_1-E_2)^2}\frac{t}{2\hbar}\right]$$

这就是拉比公式。

态间振荡

跃迁概率 $\mathscr P_{12}(t)$ 的图像为

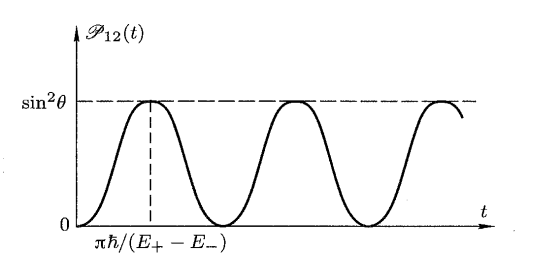
从图像上可以看出，转移概率 $\mathscr P_{12}(t)$ 以 $\frac{E_+-E_-}\hbar$ 为频率（即系统唯一的玻尔频率）随着时间振荡，极大值为 $\sin^2\theta$ 。振荡频率和极大值都是 $|W_{12}|$ 和 $\Delta=E_1-E_2$ 的函数；当 $\Delta=0$ 时，玻尔频率为 $\frac{2|W_{12}|}\hbar$ ，极大值取 $1$ ，说明在 $t=\frac{2k+1}2\frac{\pi\hbar}{|W_{12}|}$ 这些时刻，系统从 $|\varphi_1\rangle$ 演化到 $|\varphi_2\rangle$ 。

上面的分析说明，两个态之间的耦合 $W$ 使得他们之间存在随时间振荡的跃迁概率；尤其是在两个能量相等 $E_1=E_2$ 的态之间的任何耦合，总是使得系统在这两个态之间进行完整的振荡，耦合强度仅正比地影响振荡频率。

另一方面，在能级差 $E_1-E_2$ 变大时，玻尔频率也增大，但是 $\sin^2\theta$ 减小。在弱耦合 $E_1-E_2\gg|W_{12}|$ 情况下， $E_1-E_2\simeq E_+-E_-$ ， $\sin^2\theta\simeq0$ ，可见跃迁概率非常小。实际上这容易理解：因为弱耦合情况下，未微扰的态本就接近于新的定态，自然不易发生变化。

仍以 ${\rm H}_2^+$ 为例，其电子根据定域在不同的质子附近区分而具有两个能量相等的态，可知系统是在这两个态之间以玻尔频率振荡。由于电子分布不同会导致系统产生不同的电偶极矩，因此这种振荡实际上会使得整体产生振荡的电偶极矩，因而也就发生了电磁辐射。在 ${\rm H}_2^+$ 离子的吸收谱和发射谱中可以观察到这一现象。